Sin Cos Tan Cot | Bảng Công Thức Lượng Giá Lớp 9

Sin Cos Tan Cot – Bài viết chia sẻ bảng công thức lượng giác lớp 9 đầy đủ chi tiết nhất kèm phương pháp học và những bài tập ví dụ điển hình mà các bạn học sinh có thể học tập và tham khảo để làm bài tập. Với những phân tích và chia sẻ chi tiết sẽ giúp các em dễ dàng hơn trong việc năm bắt kiến thức này.

I. Sin Cos Tan Cot | Bảng Công Thức Lượng Giá Lớp 9: Khái Niệm và Bài Tập

Trong Toán học thì phần các công thức lượng giác bao gồm : Bảng lượng giác và các bài tạp lương giác lớp 9 10 và lớp 11 liên quan được dùng tương đối nhiều trong quá trình học và trong các kỳ thi. Để nắm vững và hiểu bản chất của kiến thức là điều không phải dễ. Bài viết sau của gia sư Đăng Minh sẽ phần nào giúp các khi học phần lượng giác.

Bảng công thức lượng giác đầy đủ Sin Cos Tan Cot lớp 9, 10 và lớp 11 là một trong những kiến thức Toán Học vô cùng quan trọng gắn liền với các em học sinh trong quá trình học. Các công thức Sin Cos Tan Cot đươc sử dụng rất nhiều trong các bài tập, các đề thi mà bắt buộc các học sinh đều phải biết làm. Dưới đây gia sư Đăng Minh sẽ chia sẻ những kiến thức cơ bản về bảng lượng giác đầy đủ, bảng công thức tỉ số lượng giác và các kiến thức liên quan giúp các em học sinh bổ sung thêm kiến thức.

 

Kiến thức toán học là vô tận. Nhiều bạn cho rằng, kiến thức toán học ở cấp 2 không liên quan gì nhiều đến cấp 3. Tuy nhiên, sự thật lại ngược lại như vậy, kiến thức cấp 2 và kiến thức cấp 3 có mối liên hệ rất chặt chẽ với nhau. Chúng ta có thể liên tưởng đến khi xây một căn nhà, cái móng chính là những kiến thức toán đã học ở cấp 2, còn tòa nhà phía trên, chính là kiến thức toán cấp 3. Cái nhà đó dù có đẹp, có sang trọng đến mấy mà không có một cái móng vững chắc thì chắc chắn sẽ không thể nào tồn tại lâu dài được. Cũng như việc học toán vậy, nếu những kiến thức cơ bản không nắm chắc thì sẽ không thể học được những kiến thức nâng cao và chuyên sâu.

Một trong những kiến thức toán học xuyên suốt từ những năm cuối cấp 2 đến cấp 3, thậm chí nó là một trong những kiến thức quan trọng nhất trong suốt 12 năm học, là phần kiến thức giúp các bạn “kiếm điểm” trong các “trận chiến” kì thi THPT Quốc Gia – đó chính là phần lượng giác. Bài viết sau đây sẽ tổng hợp các kiến thức về phần công thức lượng giác, Trung Tâm Gia Sư Đăng Minh hy vọng, bài viết này sẽ trở thành một trong những công cụ hỗ trợ đắc lực giúp các bạn “sĩ tử” có thể ôn luyện và tổng hợp được những kiến thức quan trọng để sẵn sàng bước vào “bước ngoặt” của cuộc đời.

Bạn cũng có thểm xem thêm các kiến thức hay khác trong mục CẨM NANG HỌC TẬP hoặc nếu muốn có gia sư để học tốt hơn có thể tham khảo bảng giá gia sư nhé.

1. Khái niệm bảng tỉ số lượng giác của một góc nhọn

 

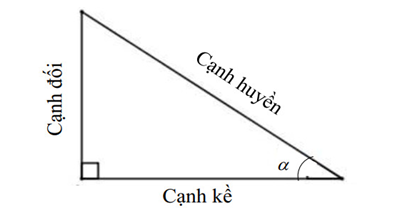
Với:

 sin : là tỉ số giữa cạnh đối và cạnh huyền của góc

 cos : là tỉ số giữa cạnh kề và cạnh huyền của góc

 tan : là tỉ số giữa cạnh đối và cạnh kề của góc

 cot : là tỉ số giữa cạnh kề và cạnh đối của góc

Mẹo học thuộc : Sin đi học, Cos không hư, Tan đoàn kết, ,Cot kết đoàn

2. Bảng công thức tỉ số lượng giác lớp 9 của một số góc đặc biệt.

a, Tỉ số lượng giác của 2 góc phụ nhau. ( α + β = 90° )

sin α  = cos β            cos α = sin β

tan α  = cot β             cot α = tan β

b, Bảng tỉ số của các góc đặc biệt.

 

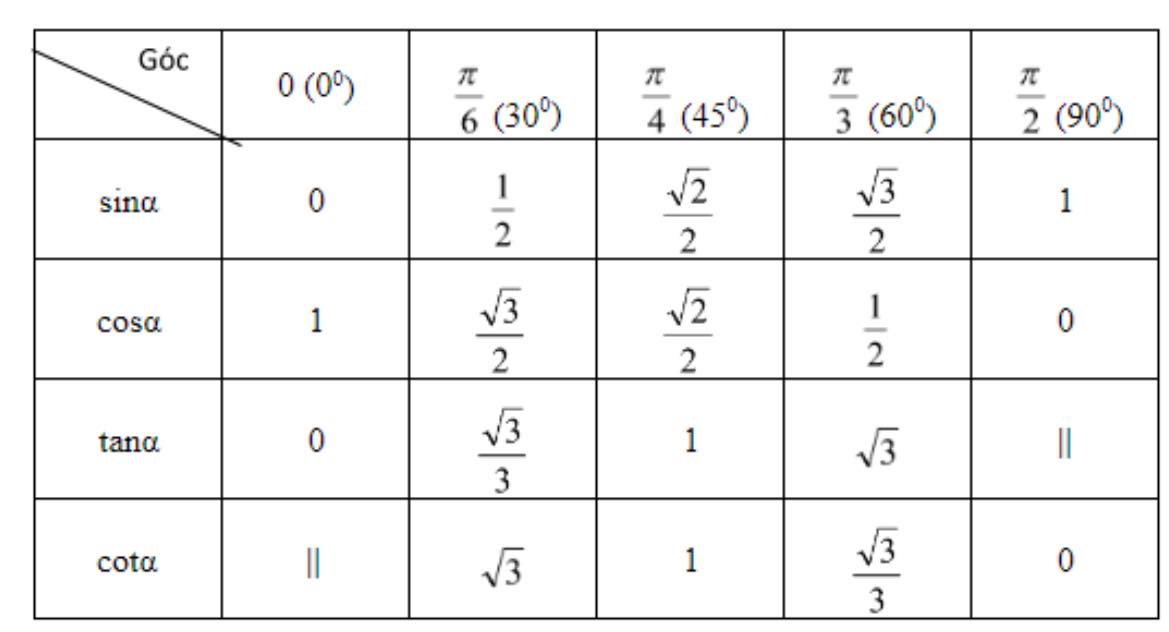
3. Bài tập vận dụng các công thức lượng giác Sin Cos Tan Cot

a, Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.

Giải :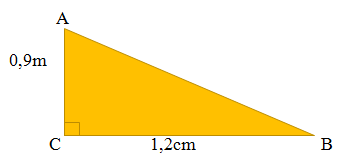 

– Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:

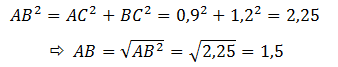
– Các tỉ số lượng giác của góc B là :

II. Bảng Các Công Thức Lượng Giác Lớp 9 Sin Cos Tan Cot Đầy Đủ và Bài Tập

Bước sang cấp 3, lượng giác không chỉ dừng lại ở các công thức cơ bản như trên, mà nó đã vươn lên một “đẳng cấp” và “tầm cao” mới, cùng với đó là vai trò “kiếm điểm” cho các bạn sĩ tử. Sau đây là phần tổng quan kiến thức lượng giác, hi vọng sẽ giúp đỡ các bạn phần nào trong việc ghi nhớ và ôn tập kiến thức một cách tốt nhất. Việc ghi nhớ  công thức lượng giác cũng như việc nhớ 7 hằng đẳng thức đáng nhớ khi các em học lớp 8, 9.

1. Bảng công thức tỉ số lượng giác lớp 10

1.1 Các công thức lượng giác cơ bản.

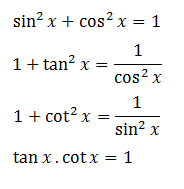
1.2. Các cung có liên quan đặc biệt.

a, Cung đối nhau:

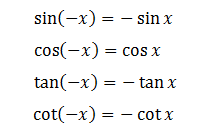
b, Cung bù nhau: x và π-x

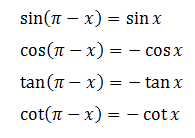c, Cung phụ nhau: x và π⁄2 – x

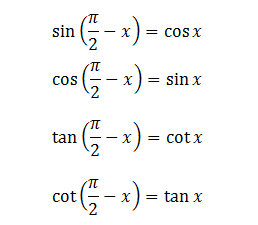d, Cung hơn kém nhau π : χ và π + χ

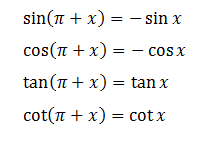
e, Cung hơn kém nhau π⁄2 : χ và χ + π⁄2

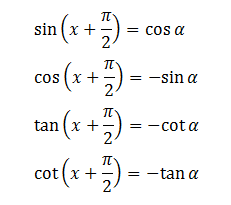
1.3. Công Thức Cộng.

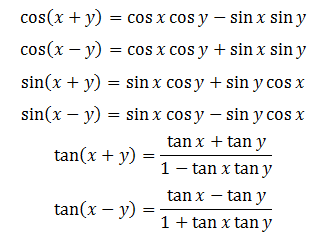
1.4. Công Thức Nhân Đôi.

 

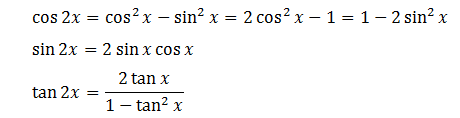
1.5. Công Thức Hạ Bậc.

 

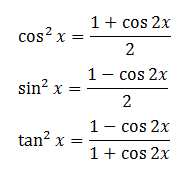
1.6. Công Thức Tính sin x, cos x, tan x theo t=tan⁡ x/2

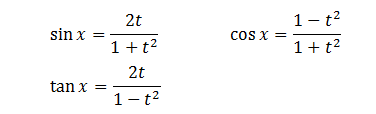
1.7. Công Thức Nhân Ba.

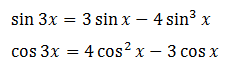
1.8. Công Thức Biến Đổi Tổng Thành Tích.

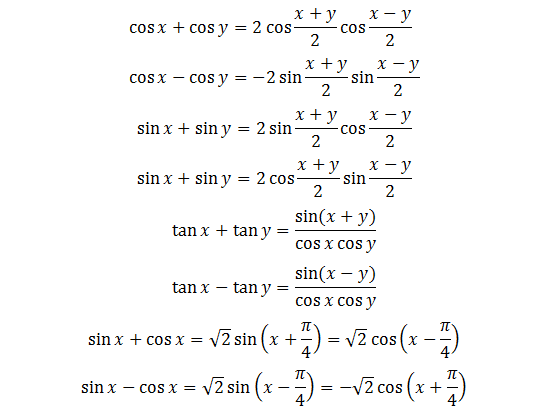
1.9. Biến Đổi Tích Thành Tổng.

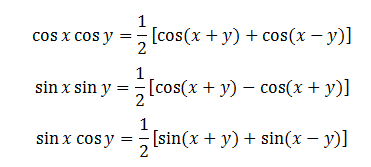
III. Tổng Hợp 200 Bài Tập Lượng Giác Sin Cos Tan Cot Có Lời Giải

IV. Một Số Kĩ Năng Cơ Bản Để Giải Phương Trình Lượng Giác

1. Giải phương trình lượng giác bằng cách đưa về phương trình tích.

a. Lưu ý :

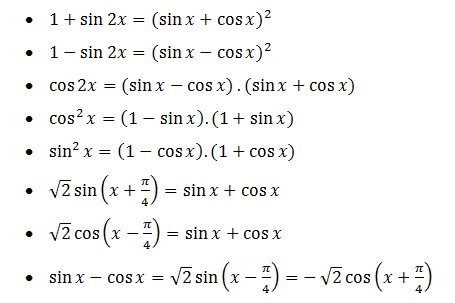b. Ví dụ.

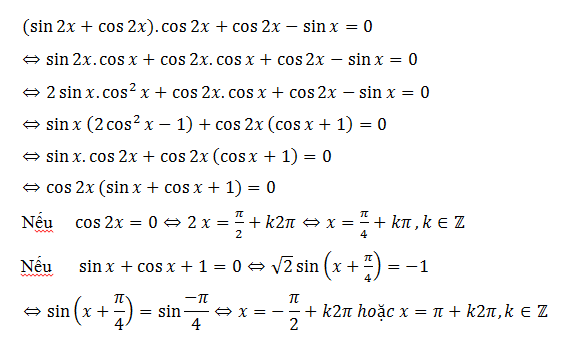
2. Giải phương trình bằng cách đưa về phương trình bậc cao đối với 1 hàm số lượng giác.

a. Lưu ý:

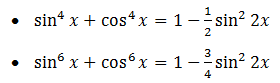b. Ví dụ:

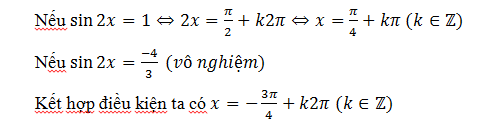
3. Giải phương trình bằng cách đưa về dạng asin⁡x+bcos⁡x

a. Dấu hiệu :

Xuất hiện √3 rồi đưa về dạng trên theo cos hoặc sin đứng sau √3

b. Ví dụ :

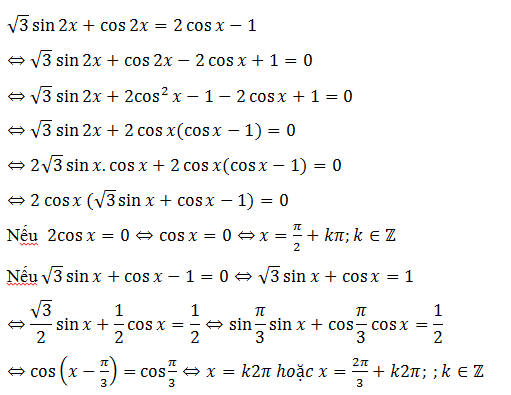
V. Một Số Mẹo Ghi Nhớ Bảng Công Thức Lượng Giác Sin Cos Tan Cot.

Với số lượng công thức lượng giác khổng lồ, việc ghi nhớ chúng chắc chắn sẽ trở thành những khó khăn đối với các bạn học sinh khi mới làm quen với lượng giác. Đôi khi, nó còn trở thành nỗi “ám ảnh” và là sự “khủng hoảng” tinh thần rất lớn. Chính vì vậy, trong phần cuối của bài viết này, chúng tôi – Trung tâm Gia Sư Đăng Minh sẽ giúp các bạn có thêm được một số mẹo hữu ích để ghi nhớ công thức. Tuy nhiên, đây chỉ là những công cụ hỗ trợ cơ bản, còn nếu các bạn muốn ghi nhớ những công thức trên một cách nhuần nhuyễn thì chỉ có một cách đó chính là: “Có công mài sắt – Có ngày nên kim”, hãy chăm chỉ luyện tập làm bài tập nhé. Chúc các bạn có một kết quả học tập tốt

Bình Luận Facebook

bình luận

.