
Trang chủ » Cẩm Nang Học Tập »
Công Thức Tính Diện Tích Tam Giác Vuông – Cân – Đều
Các em muốn tìm công thức tính diện tích tam giác vuông / diện tích tam giác cân / diện tích tam giác đều… Bài viết sau trung tâm gia sư Đăng Minh sẽ liệt kê các công thức trên cùng với những điện nghĩa, công thức và các dạng bài tập về cách tính diện tích hình tam giác. Chúc các em học tập thật tốt!
Nội dung bài viết
I. Định Nghĩa Hình Tam Giác Vuông, Cân Đều
Như các em đã thấy, tam giác là một trong những hình quen thuộc trong chương trình Toán phổ thông. Không quá khi cho rằng, hình tam giác chính là hình quan trọng bậc nhất trong chương trình Toán Hình, nhất là cấp 2 và cấp 3, vì nó đều liên quan đến các cuộc thi quan trọng. Vì thế các công thức tính diện tích tam giác vuông, tam giác cân và tam giác đều là phần kiến thức các em nên ghi nhớ.
Kiến thức về công thức và cách tính diện tích tam giác vuông, cân đều là phần quan trọng với các em học sinh lớp 5 đến 12. Có nhiều biến thể khác nhau nên các công thức và cách tính cũng sẽ nhiều hơn. Trung tâm gia sư Đăng Minh sẽ tổng hợp tất cả các công thức và cách tính diện tích các hình tam giác đầy đủ nhất để giúp các em học sinh dễ dàng học tập, ghi nhớ và áp dụng kiến thức này.
1. Hình tam giác là gì? Các tính chất của hình tam giác
a, Hình tam giác là gì?
Hình tam giác (hình có 3 cạnh) là một hình cơ bản phổ biến trong Toán Hình Học. Là hình có hai chiều phẳng và có 3 đỉnh là 3 điểm, không thẳng hàng và nối với 3 đỉnh là 3 đoạn thẳng. Trong các loại hình đa giác thì tam giác có ít cạnh nhất. Đặc điểm của tam giác luôn là một đa giác lồi và luôn là một đa giác đơn ( có tổng các góc trong luôn luôn nhỏ hơn 180°). Tam giác thường được ký hiệu là △ABC bao gồm các cạnh AB BC CA.
Trong Toán Hình Học thì hình tam giác có thể được chia thành nhiều loại khác nhau. Và để có thể phân loại người ta có thể dựa vào các yếu tốt sau:
– Chiều dài của các cạnh của hình bao gồm: Tam giác thường (không có đặc điểm chung), tam giác cân(có 2 cạnh bằng nhau), tam giác đều (có 3 cạnh, 3 góc bằng nhau)
– Dựa vào số đo các góc trong tam giác như: tam giác vuông (có 1 góc vuông), tam giác tù (có 1 góc lớn hơn 90độ), tam giác nhọn (có 3 góc nhỏ hơn 90 độ) và tam giác vuông cân (có 1 góc 90độ và 2 cảnh góc vuông bằng nhau)
b, Các tính chất của hình tam giác
Cũng như các loại hình khác trong Toán Hình Học thì hình tam giác cũng sẽ có các tính chất nhất định mà các bạn cần phải nắm rõ:
– 1 tam giác bất kỳ có tổng các góc trong bằng 180độ
– Theo định lý Pytago: Trong tam giác vuông bất kỳ thì tổng bình phương của 2 cạnh góc vuông luôn luôn bằng bình phương của cạnh huyền.
– Đường cao: Đoạn thẳng được dựng từ 1 đỉnh bất kỳ vuống góc xuống cạnh đối diện của định đó được gọi là đường cao
– Đường trung tuyến: Đoạn thẳng nối từ 1 đỉnh bất kỳ trong tam giác tới trung điểm của cạnh đổi diện được gọi là đường cao, đường cao sẽ chai tam giác thành 2 tam giác nhỏ hơn và có diện tích bằng nhau
– Đường trung trực: Đường thẳng đi qua trung điểm của 1 cạnh bất kỳ và vuông góc với cạnh đó được gọi là đường trung trực, 3 đường trung trực sẽ giao nhau lại trọng tâm của tâm giác. Điểm trọng tâm này sẽ cách đều 3 đỉnh của tam giác đó
– Đường phân giác: Đường thẳng đi qua 1 góc của tam giác và chia đều góc đó thành 2 góc bằng nhau được gọi là đường phân giác
– Trong một hình tam giác thì cạnh lớn hơn sẽ là cạnh đối diện với góc lớn hơn
– Điểm mà ba đường trung tuyến giao nhau sẽ là trọng tâm của tam giác
– Điểm mà ba đường phân giác giao nhau sẽ là tâm của đường tròn nội tiếp tam giác
– Điểm giao nhau của ba đường trung trực là tâm của đường tròn ngoại tiếp tam giác
– Tỷ lệ giữ Sin của góc đối điện và độ dài của mỗi cạnh tam giác là như nhau
– Đường phân giác của một góc trong tam giác sẽ luôn luôn chia cạnh đối diện góc đó thành hai đoạn thẳng có tỉ lệ với chính hai cạnh kề của hai đoạn thẳng đó trong tam giác
– Hiệu số độ dài của 2 cạnh trong 1 tam giác luôn luôn nhỏ hơn độ dài của 1 trong 2 cạnh đó và đồng thời sẽ nhỏ hơn tổng độ dài của 2 cạnh
– Điểm giao nhau của ba đường cao trong tam giác được gọi lại trực tâm
– Bình phương của độ dài một cạnh bất kỳ của tam giác bằng tổng bình phương của độ dài hay cạnh còn lại và trừ đi hai lần tích của độ dài hai cạnh đó với cosin của góc xen giữa chính hai cạnh đó.
– Đoạn thẳng nối trung điểm của hai cạnh tam giác là đường trung bình của tam giác đó
c, Hình tam giác thường
– Hình tam giác là hình được tạo bởi 3 cạnh, chính là 3 đường thẳng nối 3 đỉnh của hình đó.
– ABC có:
+ 3 cạnh: cạnh AB, cạnh BC, cạnh AC
+ 3 đỉnh: đỉnh A, đỉnh B, đỉnh C
+ 3 góc:
- Góc đỉnh A (gọi tắt là góc A), góc tạo bởi cạnh AB và cạnh AC.
- Góc đỉnh B (gọi tắt là góc B), góc tạo bởi cạnh AB và cạnh BC.
- Góc đỉnh C (gọi tắt là góc C), góc tạo bởi cạnh BC và cạnh AC.
2, Các loại hình tam giác thường gặp:
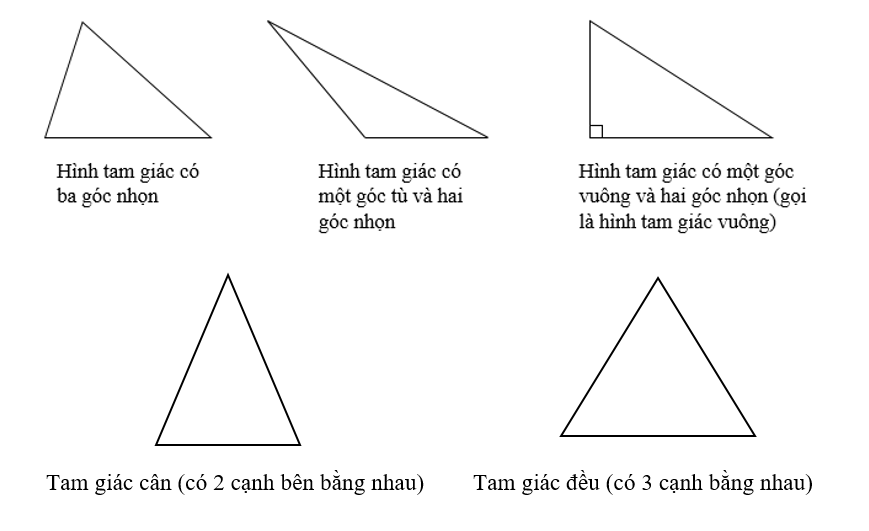
3, Tính chất của đường cao và đáy
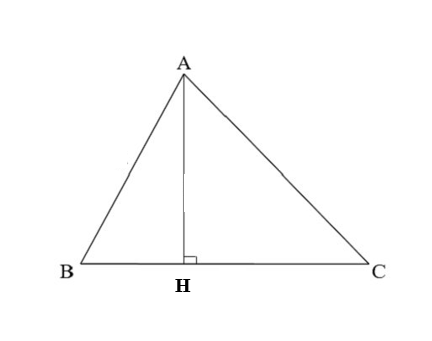
- Xét tam giác ABC có:
- BC là đáy
AH là đường cao ứng với đáy BC
(độ dài AH chính là độ dài chiều cao của tam giác ABC
II. Công Thức Tính Diện Tích Hình Tam Giác Vuông – Cân – Đều.
1, Công thức tính diện tích hình tam giác:
Muốn tính diện tích hình tam giác Vuông Cân Đều, ta lấy độ dài của cạnh đáy nhân với độ dài chiều cao rồi chia cho 2 (lưu ý độ dài 2 cạnh phải có cùng đơn vị đo)
+ TH1: Công thức và cách tính diện tích tam giác thường
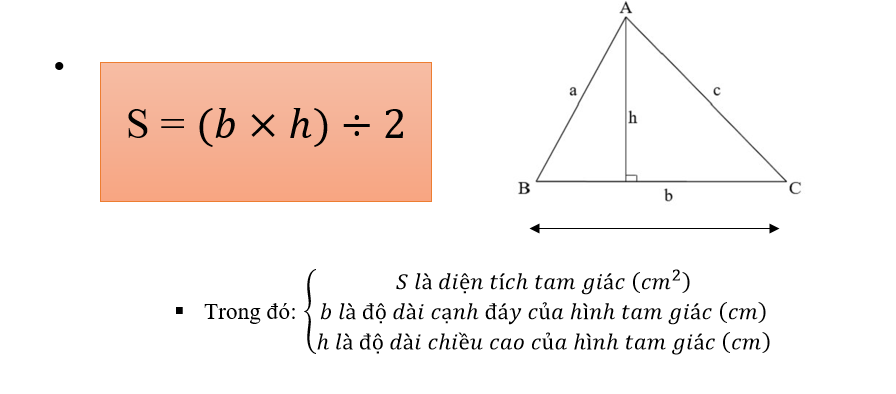
+ TH2: Công thức và cách tính diện tích tam giác vuông
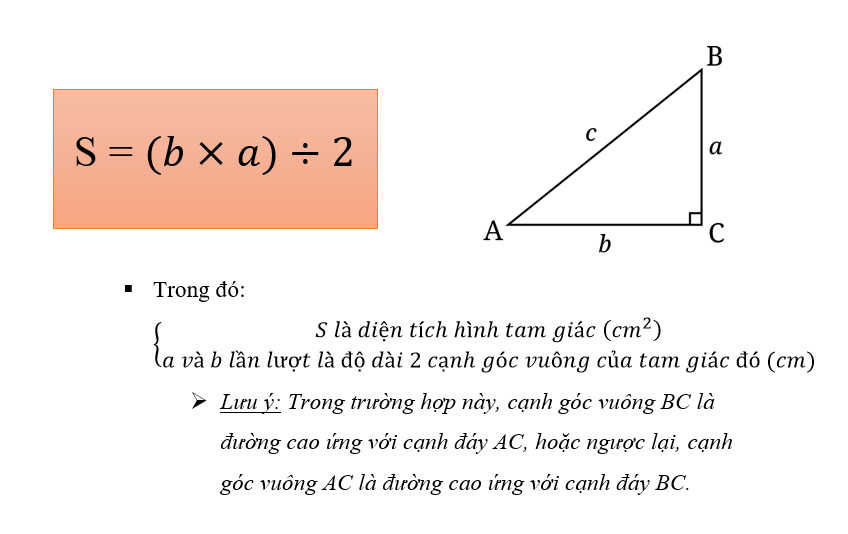
• Mở rộng:
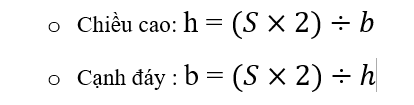
III. Các Dạng Bài Tập về Công Thức Tính Diện Tích Tam Giác Vuông – Cân – Đều
Dạng 1: Xác định đáy và đường cao của các tam giác.
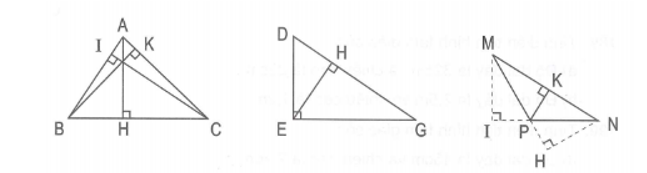
VD1: Xác định đáy và đường cao của các tam giác sau:
- Giải:
- Hình 1: AH là đường cao ứng với cạnh đáy BC.
BK là đường cao ứng với cạnh đáy AC.
CI là đường cao ứng với cạnh đáy AB. - Hình 2: EH là đường cao ứng với cạnh đáy DG.
DE là đường cao ứng với cạnh đáy EG.
EG là đường cao ứng với cạnh đáy DE. - Hình 3: MI là đường cao ứng với cạnh đáy PN.
PK là đường cao ứng với cạnh đáy MN.
NH là đường cao ứng với cạnh đáy MP.
- Hình 1: AH là đường cao ứng với cạnh đáy BC.
VD2: Xác định đường cao của tam giác tương ứng với đáy BC cho trước rồi viết theo mẫu.
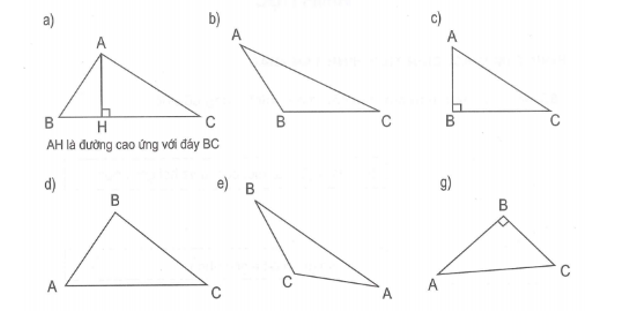
=> Giải:
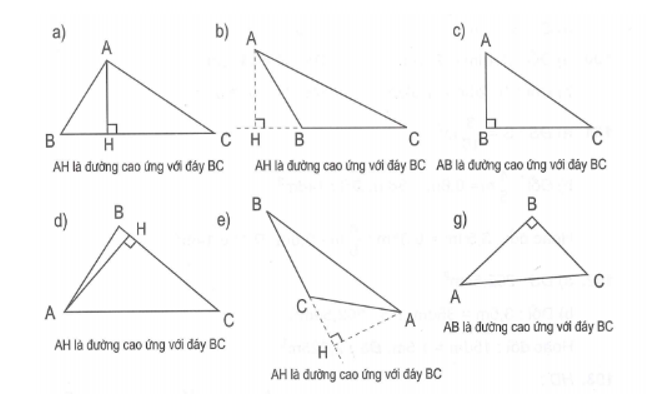
Dạng 2: Cách tính diện tích hình tam giác vuông – cân – đều.
VD1: Một hình tam giác có đáy là 20cm và chiều cao là 8cm. Hãy tính diện tích hình tam giác đó?
- Giải:
Diện tích hình tam giác đó là:
(20 x 8):2 = 80 (
Đáp số: 80
VD2: Một hình tam giác có đáy là 15cm và chiều cao là 40mm. Hãy tính diện tích hình tam giác đó?
- Giải: Đổi 40mm = 4cm
Diện tích hình tam giác đó là:
(15 x 4):2 = 30 (
Đáp số: 80
VD3: Một mảnh vườn hình tam giác có diện tích 225cm2 và cạnh đáy 15cm. Hãy tính chiều cao mảnh vườn đó?
- Giải:
Chiều cao mảnh vườn đó là:
(225 x 2): 15 = 30 (cm)
Đáp số: 30 cm
VD4: Một tấm biển báo hình tam giác có tổng cạnh đáy và chiều cao là 58cm, cạnh đáy hơn chiều cao 22cm. Tính diện tích tấm bảng quảng cáo đó ?
- Giải:
Độ dài cạnh đáy là:
(58 + 22) : 2 = 40 (cm)
Độ dài chiều cao là:
58 – 40 = 18 (cm)
Diện tích tấm biển báo là:
(40 x 18) : 2 = 720 (cm2)
Đáp số: 720 cm2
VD5: Một hình chữ nhật có diện tích là 750cm2 và diện tích này bằng 60% diện tích của hình tam giác. Hãy tính cạnh đáy của hình tam giác đó, biết chiều cao của hình tam giác này là 12,5dm ?
- Giải:
Đổi: 12,5dm = 125m
Diện tích hình tam giác là:
750 : 60% = 1250 (cm2)
Cạnh đáy hình tam giác là:
1250 x 2 : 125 = 20 (cm)
Đáp số: 20cm
VD 6: Tính diện tích hình tam giác vuông ABC
Cho tam giác ABC vuông góc tại A, chu vi là 39cm. Cạnh AB bằng cạnh BC, cạnh AC bằng cạnh BC. Tính diện tích hình tam giác ABC ?
- Giải:
Ta có: và
Ta có cạnh BC là 20 phần bằng nhau thì
cạnh AB là 15 phần và cạnh AC là 4 phần.
Độ dài cạnh AB là:
39 : (20 + 15 + 4) x 15 = 15 (cm)
Độ dài cạnh BC là:
39 : (20 + 15 + 4) x 20 = 20 (cm)
Độ dài cạnh AC là:
39 – 15 – 20 = 4 (cm)
Diện tích hình tam giác ABC là:
15 x 4 : 2 = 30 (cm2)
Đáp số: 30 cm2
VD7: Một miếng đất hình tam giác có chiều cao là 20 m. Hỏi nếu kéo dài đáy của miếng đất đó thêm 5 m thì diện tích sẽ tăng thêm bao nhiêu m2?
- Giải:
Nếu kéo dài đáy của miếng đất đó thêm 5m thì diện tích của miếng đất sẽ tăng thêm là:
20 x 5 : 2 = 50 (m2)
Đáp số: 50m2
VD8: Một hình tam giác ABC có cạnh đáy là 5,6m. Nếu kéo dài cạnh đáy BC thêm 3,4m thì diện tích tam giác đó tăng thêm 5,265 m2. Hãy tính diện tích hình tam giác ABC đó ?
- Giải:
Độ dài chiều cao của hình tam giác đó là:
5,265 x 2 : 3,4 = 3,9 (m)
Diện tích hình tam giác ABC là:
5,6 x 3,9 : 2 = 10,92 (m2)
Đáp số: 10,92 m2
Sau bài viết hướng dẫn học về Hình Tròn Công Thức Tính Diện Tích Hình Tròn, Chu Vi Hình Tròn và Công Thức Diện Tích Hình Thang, Chu Vi Hình Thang & Bài Tập thì hôm nay, Gia Sư Đăng Minh – Trung tâm gia sư Đăng Minh sẽ giúp các em ôn tập lại những kiến thức cơ bản nhất về hình tam giác, giúp các em xây dựng được những nền móng vững chắc khởi đầu để có thể từng bước, từng bước chinh phục những bài toán từ dễ đến khó về hình tam giác sau này.
Bình Luận Facebook
Tư vấn gia sư (24/7) 097.948.1988

Các tin liên quan
- TOP 10 câu hội thoại tiếng Anh phổ biến nhất 2016
- Cách Tính Điểm Tốt Nghiệp Năm 2021 Mới Nhất
- Lập Dàn Ý và Bài Văn Mẫu Giải Thích Nhan Đề “Những Ngôi Sao Xa Xôi”
- Lập Dàn Ý và Bài Văn Tả Bà Hay Nhất Của HS Giỏi 2024
- 6+ Cách Học Giỏi Văn Khoa Học Từ Các Thủ Khoa Khối C
- Dàn Ý Nghị Luận Trao Duyên Và Bài Văn Nghị Luận Bài Trao Duyên
- Dàn Ý Bài Văn Tả Giờ Ra Chơi Hàng Ngày Của Trường Em
- Kinh Nghiệm Học Tiếng Anh SIÊU hiệu quả
Phụ huynh quan tâm
- Địa chỉ cung cấp giáo viên dạy văn giỏi cấp 2 ở hà nội
- Gia Sư Tiếng Anh Online (Dạy kèm 1-1 an toàn chống dịch)
- Gia Sư Dạy Đàn Organ Tại Nhà Hà Nội (Học phí gia sư 2024)
- Gia sư Nhân Trí : Nhân Cách và trí tuệ tạo nên gia sư giỏi
- Dàn Ý Tả Dòng Sông Quê Em và Bài Văn Tả Con Sông Hay Nhất 2024
- TOP 3 Tiêu Chí Chọn Gia Sư Tiếng Anh Luyện Thi Đại Học
- Kinh Nghiệm Tìm Giáo Viên Dạy Đàn Organ Tại Nhà Cho Con
- Trung Tâm Gia Sư tại khu đô thị Trung Văn Vinaconex 3





